Witaj w dziale "Fizyka na Lekko"!
Wybierz temat z panelu po lewej stronie, aby wyświetlić lekcję.
Znajdziesz tu przystępne wyjaśnienia trudnych zagadnień fizycznych, przykłady i wzory.
W fizyce, aby opisać ruch ciała, musimy najpierw określić jego układ odniesienia, czyli punkt, względem którego obserwujemy jego położenie. Dzięki temu wiemy, że ruch jest względny, ponieważ ciało może być w ruchu względem jednego obiektu, a w spoczynku względem innego (np. pasażer siedzący w pociągu jest w spoczynku względem wagonu, ale w ruchu względem drzew, które mijają za oknem).)
Ruch odbywa się po określonym torze, który może być prostą lub krzywą. Droga (s) to całkowita długość tego toru i jest to wielkość skalarna (ma tylko wartość). Natomiast przemieszczenie ( d) to wektor, który łączy punkt początkowy z końcowym, i jest wielkością wektorową (ma wartość, kierunek i zwrot)
Prędkość (v) mówi nam, jak szybko zmienia się położenie ciała. Wyróżniamy prędkość średnią (na całej trasie) i prędkość chwilową (w danym momencie, pokazywaną np. przez prędkościomierz)
Przyspieszenie (a) to wielkość, która opisuje, jak szybko zmienia się prędkość ciała w czasie.
Podstawowe pojęcia
- Prędkość: to stosunek pokonanej drogi do czasu, w którym została pokonana.
- Przyspieszenie: to wielkość opisująca, jak szybko zmienia się prędkość ciała.
Prędkość
Wzór ten pozwala obliczyć prędkość, z jaką poruszało się ciało.
$$v=\frac{s}{t}$$
Przykład:
Rowerzysta pokonał 100 metrów w 20 sekund. Z jaką prędkością się poruszał?
Rozwiązanie:$$v=\frac{100 m}{20 s}=5\frac{m}{s}$$
Przyspieszenie
Wzór ten służy do obliczenia, jak szybko zmieniała się prędkość ciała w danym czasie.
$$a=\frac{Δv}{Δt}$$
Przykład:
Samochód w ciągu 4 sekund zwiększył prędkość o 20 m/s. Jakie było jego przyspieszenie?
Rozwiązanie:$$a=\frac{20\frac{m}{s}}{4 s}=5\frac{m}{s^2}$$
Jest to najprostszy rodzaj ruchu. Ciało porusza się w nim ze stałą prędkością, po linii prostej. Oznacza to, że jego prędkość (zarówno wartość, jak i kierunek) nie zmienia się w czasie. Właśnie dlatego w tym ruchu przyspieszenie jest równe 0.
Podstawowe pojęcia
- Prędkość: w tym ruchu prędkość jest stała.
- Przyspieszenie: jest równe 0, ponieważ prędkość się nie zmienia.
- Droga: rośnie proporcjonalnie do czasu.
Droga
Wzór ten pozwala obliczyć drogę, jaką pokonało ciało w ruchu ze stałą prędkością.
$$s=\frac{v}{t}$$
Przykład:
Samochód jedzie ze stałą prędkością 60 km/h. Jaką drogę pokona w ciągu 2 godzin?
Rozwiązanie:$$s=\frac{60\frac{km}{h}}{2 h}=120 km$$
To ruch, w którym prędkość ciała zmienia się o taką samą wartość w każdej jednostce czasu. Oznacza to, że ciało porusza się ze stałym przyspieszeniem. Przykładem jest swobodny spadek kamienia, który co sekundę zwiększa swoją prędkość o około 9,81 m/s.
Podstawowe pojęcia
- Przyspieszenie: w tym ruchu jest stałe i różne od zera. Może być dodatnie (przyspieszanie) lub ujemne (opóźnianie).
- Prędkość: zmienia się w czasie, rosnąc lub malejąc.
- Droga: nie rośnie proporcjonalnie do czasu, jak w Ruch jednostajny prostoliniowy, ale szybciej.
Prędkość w dowolnej chwili
Ten wzór pozwala obliczyć prędkość ciała w dowolnym momencie czasu, znając jego prędkość początkową, przyspieszenie i czas.
$$v=v_0 + a ⋅ t$$
Przykład:
Samochód rusza z miejsca z przyspieszeniem 2 m/s². Jaką prędkość osiągnie po 5 sekundach?
Rozwiązanie:$$v=0\frac{m}{s} + 2\frac{m}{s^2} ⋅ 5 s=10\frac{m}{s} $$
Droga (bez prędkości początkowej)
Wzór ten pozwala obliczyć drogę, jaką pokonało ciało, które ruszało z miejsca.
$$s=\frac{1}{2}a ⋅t^2$$
Przykład:
Zjeżdżający na sankach chłopiec, ruszając z miejsca, porusza się z przyspieszeniem 1,5 m/s². Jaką drogę przejedzie w ciągu 4 sekund?
Rozwiązanie:$$s=\frac{1}{2} ⋅ 1,5\frac{m}{s^2} ⋅ (4s)^2 = \frac{1}{2} ⋅ 1,5 ⋅ 16 = 12 m$$
To ruch, w którym ciało porusza się po torze w kształcie okręgu. Może być to ruch jednostajny po okręgu, gdy prędkość ma stałą wartość, lub ruch zmienny, gdy wartość prędkości się zmienia. Nawet w ruchu jednostajnym po okręgu, ciało ma przyspieszenie, bo ciągle zmienia się kierunek jego prędkości.
Podstawowe pojęcia
- Prędkość liniowa: opisuje, jak szybko ciało porusza się po okręgu. Wektor prędkości jest zawsze styczny do toru ruchu.
- Prędkość kątowa: opisuje, jak szybko ciało obraca się wokół środka okręgu. Mierzy się ją w radianach na sekundę.
- Okres: czas potrzebny na wykonanie jednego pełnego obiegu po okręgu.
- Częstotliwość: liczba pełnych obiegów wykonanych w jednostce czasu.
- Przyspieszenie dośrodkowe: przyspieszenie skierowane do środka okręgu, które odpowiada za zmianę kierunku wektora prędkości.
Prędkość liniowa
Wzór ten pozwala obliczyć prędkość, z jaką porusza się obiekt po okręgu, znając jego promień (r) i okres (T).
$$v=\frac{2πr}{T}$$
Przykład:
Samochód porusza się po rondzie o promieniu 20 m. Okrążenie zajmuje mu 10 sekund. Jaka jest jego prędkość?
Rozwiązanie:$$v=\frac{2 ⋅ π ⋅ 20 m}{10 s} = 4π \frac{m}{s}\approx 12,57\frac{m}{s}$$
Przyspieszenie dośrodkowe
Wzór ten pozwala obliczyć przyspieszenie, które zmienia kierunek prędkości. Jest ono tym większe, im większa prędkość i mniejszy promień okręgu.
$$a_d=\frac{v^2}{r}$$
Przykład:
Kamień kręcony na sznurku z prędkością 3 m/s po okręgu o promieniu 0,5 m. Jakie jest jego przyspieszenie dośrodkowe?
Rozwiązanie:$$a_d=\frac{(3\frac{m}{s^2})^2}{0,5 m} = \frac{9}{0,5} = 18\frac{m}{s^2}$$
W fizyce ruch jest zawsze pojęciem względnym, co oznacza, że to, czy dany obiekt się porusza, zależy od wybranego układu odniesienia. Jeśli pasażerowie w pociągu widzą, jak drzewa i domy za oknem pędzą w przeciwnym kierunku, to dla nich te obiekty są w ruchu. Jednocześnie, dla osoby stojącej na peronie, pociąg jest w ruchu, a drzewa i domy pozostają w spoczynku.
Podstawowe pojęcia
- Układ odniesienia: to punkt lub zbiór punktów, względem którego opisujemy ruch.
- Prędkość względna: prędkość jednego ciała względem drugiego.
Prędkość względna (ruch w przeciwnych kierunkach)
Wzór ten stosujemy, gdy ciała poruszają się w przeciwnych kierunkach. Ich prędkości względem siebie się sumują.
$$v_{wzgl}=v_A + v_B$$
Przykład:
Dwa pociągi jadą w przeciwnych kierunkach. Pociąg A jedzie z prędkością 80 km/h, a pociąg B z prędkością 70 km/h. Z jaką prędkością pociąg A porusza się względem pociągu B?
Rozwiązanie:$$v_{wzgl}=80\frac{km}{h} + 70\frac{km}{h} = 150\frac{km}{h}$$
Prędkość względna (ruch w tym samym kierunku)
Wzór ten stosujemy, gdy ciała poruszają się w tym samym kierunku. Ich prędkości względem siebie się odejmują.
$$v_{wzgl}=v_A - v_B$$
Przykład:
Dwa samochody jadą w tym samym kierunku. Samochód A jedzie z prędkością 100 km/h, a samochód B z prędkością 80 km/h. Z jaką prędkością samochód A porusza się względem samochodu B?
Rozwiązanie:$$v_{wzgl}=100\frac{km}{h} - 80\frac{km}{h} = 20\frac{km}{h}$$
I Zasada Dynamiki Newtona
Ta zasada mówi, że ciało, na które nie działają żadne siły lub siły te się równoważą, pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Mówiąc prościej, jeśli nic nie przeszkadza, ciało "chce" zachować swój stan ruchu.
Podstawowe pojęcia
- Bezwładność: to naturalna właściwość każdego ciała, polegająca na dążeniu do zachowania swojego stanu ruchu. Im większa masa ciała, tym większa jego bezwładność.
- Siła wypadkowa: suma wszystkich sił działających na ciało. W przypadku braku ruchu lub ruchu jednostajnego prostoliniowego, siła wypadkowa jest równa zero.
II Zasada Dynamiki Newtona
Jeśli na ciało działa stała, niezrównoważona siła, to ciało porusza się z przyspieszeniem. Przyspieszenie to jest wprost proporcjonalne do działającej siły i odwrotnie proporcjonalne do masy ciała. Im większa siła, tym większe przyspieszenie. Im większa masa, tym mniejsze przyspieszenie.
Podstawowe pojęcia
- Siła: przyczyna zmiany prędkości ciała. Jednostką siły jest niuton [N].
- Masa: miara bezwładności ciała.
- Przyspieszenie: zmiana prędkości w czasie.
Siła
Wzór ten pozwala obliczyć siłę potrzebną do nadania masie określonego przyspieszenia.
$$F=m ⋅ a$$
Przykład:
Jaka siła jest potrzebna, aby ciału o masie 10 kg nadać przyspieszenie 2 m/s²?
Rozwiązanie:$$F=10 kg ⋅ 2\frac{m}{s^2}=20 N$$
III Zasada Dynamiki Newtona
Zasada ta mówi, że gdy jedno ciało działa siłą na drugie, to drugie ciało działa na pierwsze siłą o takiej samej wartości, tym samym kierunku, ale o przeciwnym zwrocie. Te siły zawsze występują w parach i działają na dwa różne ciała.
Podstawowe pojęcia
- Akcja: siła, z jaką pierwsze ciało działa na drugie.
- Reakcja: siła, z jaką drugie ciało działa na pierwsze.
Wzór
Wzór ten symbolizuje, że siła akcji ma taką samą wartość i kierunek, ale przeciwny zwrot niż siła reakcji
$$F_{akcji}=-F_{reakcji}$$
Przykład:
Siedzisz na krześle. Jaka siła działa na podłogę i jakiej siły doświadczasz od podłogi?
Rozwiązanie: Zgodnie z III zasadą, siła, z jaką naciskasz na krzesło (i podłogę) jest równa sile, z jaką krzesło (i podłoga) działa na ciebie. Te siły mają tę samą wartość, ale przeciwny zwrot.
Siła grawitacji
To siła, z jaką Ziemia przyciąga wszystkie ciała. To dzięki niej przedmioty spadają na ziemię, a my sami pozostajemy na jej powierzchni. Siła grawitacji jest bezpośrednio powiązana z masą ciała.
Podstawowe pojęcia
- Ciężar: siła, z jaką grawitacja przyciąga ciało. Wartość ciężaru zależy od masy ciała i przyspieszenia ziemskiego.
- Masa: jest cechą stałą danego obiektu, niezależną od miejsca, w którym się znajduje
- Przyspieszenie ziemskie: Przybliżona wartość przyspieszenia, z jakim swobodnie spadają ciała w pobliżu Ziemi.
Ciężar
Wzór ten pozwala obliczyć ciężar ciała, mnożąc jego masę przez przyspieszenie ziemskie.
$$Q=m ⋅ g$$
Przykład:
Jaką siłą grawitacji Ziemia przyciąga książkę o masie 0,5 kg?
Rozwiązanie:$$Q=0,5 kg ⋅ 9,81\frac{m}{s^2}\approx4,9 N$$
Siła sprężystości
Jest to siła, która powstaje w ciałach odkształconych sprężyście, na przykład w rozciągniętej sprężynie. Dąży ona do przywrócenia ciału pierwotnego kształtu.
Podstawowe pojęcia
- Współczynnik sprężystości: wartość, która charakteryzuje sprężynę. Im większy k, tym bardziej "twarda" jest sprężyna.
- Wydłużenie/skrócenie: długość, o jaką sprężyna została rozciągnięta lub ściśnięta.
Siła sprężystości (prawo Hooke'a)
Wzór ten opisuje siłę sprężystości, która jest wprost proporcjonalna do wydłużenia lub skrócenia. Znak minus oznacza, że siła sprężystości ma zawsze przeciwny zwrot do kierunku odkształcenia.
$$F_s=-k ⋅ x$$
Przykład:
Jaka siła jest potrzebna, aby rozciągnąć sprężynę o 0,1 m, jeśli jej współczynnik sprężystości wynosi 20 N/m?
Rozwiązanie:$$F_s=20\frac{N}{m} ⋅ 0,1 m = 2 N$$
Siła tarcia
To siła, która występuje, gdy powierzchnie dwóch ciał stykają się ze sobą i poruszają się względem siebie. Zawsze działa w kierunku przeciwnym do ruchu.
Podstawowe pojęcia
- Współczynnik tarcia: wartość, która zależy od rodzaju stykających się powierzchni.
- Siła nacisku: siła, z jaką jedno ciało naciska na drugie. Na poziomej powierzchni jest ona równa sile ciężkości.
Siła tarcia kinetycznego
Wzór ten pozwala obliczyć siłę tarcia, która działa na poruszające się ciało.
$$T_k=μ_k ⋅ N$$
Przykład:
Jaka siła tarcia działa na sanki o masie 10 kg, jeśli jadą po śniegu, a współczynnik tarcia kinetycznego wynosi 0,05?
Rozwiązanie:Najpierw obliczamy siłę nacisku (N), która jest równa ciężarowi sanek: $$N=Q=m ⋅ g=10 kg ⋅ 9,81\frac{m}{s^2}\approx98,1 N$$
Następnie obliczamy siłę tarcia: $$T_k=0,05 ⋅ 98,1 N \approx 4,9 N$$
Pęd to wielkość fizyczna, która opisuje ruch ciała. Można go potraktować jako "ilość ruchu" ciała. Jest to wielkość wektorowa, co oznacza, że ma wartość, kierunek i zwrot. Im większa masa i prędkość ciała, tym większy jest jego pęd.
Podstawowe pojęcia
- Pęd: iloczyn masy i prędkości ciała.
- Zasada zachowania pędu: w układzie odizolowanym (na który nie działają żadne siły zewnętrzne), całkowity pęd układu ciał jest stały.
Pęd
Wzór ten pozwala obliczyć pęd ciała, mnożąc jego masę przez prędkość.
$$p = m ⋅ v$$
Przykład:
Z jaką prędkością porusza się ciało o masie 5 kg, jeśli jego pęd wynosi 20 kg·m/s?
Rozwiązanie:$$v = \frac{20 kg ⋅ \frac{m}{s}}{5 kg} = 4 \frac{m}{s}$$
Zasada zachowania pędu
Całkowity pęd układu ciał przed zderzeniem jest równy całkowitemu pędowi po zderzeniu.
$$P_{przed} = P_{po}$$
lub $$m_1 ⋅ v_1 + m_2 ⋅ v_2 = m_1 ⋅ v_1^′ + m_2 ⋅ v_2^′$$
Przykład:
Dwie kulki zderzają się ze sobą. Kulka A o masie 2 kg porusza się z prędkością 5 m/s, a kulka B o masie 3 kg jest w spoczynku. Jaką prędkość będą miały kulki po zderzeniu, jeśli połączą się w jedno ciało?
Rozwiązanie: Obliczamy pęd układu przed zderzeniem: $$P_{przed} = 2 kg ⋅ 5\frac{m}{s} + 3 kg ⋅ 0\frac{m}{s} = 10 kg ⋅ \frac{m}{s}$$
Pęd po zderzeniu będzie taki sam, ale masa będzie sumą mas obu kulek: $$P_{po} = (m_A + m_B) ⋅ v^′$$ $$v^′ = \frac{P_{po}}{m_A + m_B} = \frac{10 kg ⋅ \frac{m}{s}}{2 kg + 3 kg} = \frac{10}{5} + 2\frac{m}{s}$$
To siła, która jest potrzebna do utrzymania ciała w ruchu po okręgu. Siła dośrodkowa jest zawsze skierowana do środka okręgu i to ona powoduje ciągłą zmianę kierunku prędkości. Bez tej siły ciało poruszałoby się wzdłuż prostej, zgodnie z pierwszą zasadą dynamiki Newtona.
Podstawowe pojęcia
- Siła dośrodkowa: siła, która powoduje zakrzywianie toru ruchu i utrzymuje ciało na okręgu.
- Przyspieszenie dośrodkowe: to przyspieszenie, którego źródłem jest siła dośrodkowa. Zmienia ono kierunek, ale nie wartość prędkości.
Siła dośrodkowa
Wzór ten pozwala obliczyć siłę potrzebną do utrzymania masy w ruchu po okręgu o promieniu z prędkością. Zauważ, że siła ta jest tym większa, im większa jest prędkość i masa ciała, a im mniejszy jest promień okręgu.
$$F_d = m ⋅ a_d = \frac{m ⋅ v^2}{r}$$
Przykład:
Kamień o masie 0,5 kg jest kręcony na sznurku po okręgu o promieniu 0,5 m z prędkością 3 m/s. Jaką siłę dośrodkową musi działać sznurek, aby utrzymać kamień w ruchu?
Rozwiązanie:$$F_d=\frac{0,5 kg ⋅ (3\frac{m}{s})^2}{0,5 m} = \frac{0,5 ⋅ 9}{0,5} = 9N$$
Praca
Praca jest wykonywana, gdy siła przesuwa ciało na pewną odległość w kierunku działania tej siły. Jeśli pchasz biurko i przesuwasz je o metr, wykonujesz pracę. Jeśli jednak pchasz ścianę, która się nie rusza, to mimo wysiłku, z fizycznego punktu widzenia, nie wykonujesz pracy.
Podstawowe pojęcia
- Praca: wartość, która opisuje, ile energii zostało przekazane lub zużyte.
- Siła: działa na ciało.
- Droga: odległość, na jaką ciało zostało przesunięte.
Praca
Wzór ten pozwala obliczyć pracę, mnożąc siłę przez drogę, na jaką ciało zostało przesunięte w kierunku tej siły.
$$W = F ⋅ s$$
Przykład:
Jaką pracę wykonała osoba, która pchała biurko siłą 50 N na odległość 2 metrów?
Rozwiązanie:$$W = 50 N ⋅ 2 m = 100 J$$
Moc
Moc mówi nam o tym, jak szybko praca została wykonana. Im szybciej wykonasz daną pracę, tym większą masz moc.
Podstawowe pojęcia
- Moc: wartość, która opisuje tempo wykonywania pracy.
- Praca: wartość opisująca wykonaną pracę.
- Czas: czas, w jakim praca została wykonana.
Moc
Wzór ten pozwala obliczyć moc, dzieląc wykonaną pracę przez czas, w jakim została ona wykonana.
$$P=\frac{W}{t}$$
Przykład:
Silnik wykonał pracę 1200 J w ciągu 6 sekund. Jaką moc ma ten silnik?
Rozwiązanie:$$P=\frac{1200 J}{6 s}= 200 W$$
Energia
Energia to zdolność do wykonania pracy. Im więcej energii ma ciało, tym więcej pracy może wykonać. Istnieje wiele form energii, ale w tej lekcji skupimy się na dwóch głównych rodzajach energii mechanicznej./p>
Podstawowe pojęcia
- Energia kinetyczna: energia, jaką posiada ciało z powodu swojego ruchu. Im większa masa i prędkość, tym większa energia kinetyczna.
- Energia potencjalna grawitacji: energia, jaką posiada ciało z powodu swojego położenia w polu grawitacyjnym (np. na pewnej wysokości). Im większa masa i wysokość, tym większa energia potencjalna.
Energia kinetyczna
Wzór ten pozwala obliczyć energię, jaką ma ciało dzięki swojemu ruchowi. Zauważ, że energia rośnie z kwadratem prędkości.
$$E_k=\frac{1}{2}m⋅v^2$$
Przykład:
Dziecko o masie 20 kg jedzie na rowerze z prędkością 5 m/s. Ile ma energii kinetycznej?
Rozwiązanie:$$E_k=\frac{1}{2} ⋅ 20kg ⋅ (5\frac{m}{s})^2 =\frac{1}{2}⋅20⋅25=250 J$$
Energia potencjalna grawitacji
Wzór ten pozwala obliczyć energię, jaką ma ciało dzięki swojemu położeniu (wysokości).
$$E_p=m⋅g⋅h$$
Przykład:
Książka o masie 0,5 kg leży na półce na wysokości 1,5 metra. Ile ma energii potencjalnej?
Rozwiązanie:$$E_p=0,5kg⋅9,81\frac{m}{s^2}⋅1,5m \approx7,36J$$
Zasada zachowania energii mówi, że energia nie może być ani stworzona, ani zniszczona, może jedynie zmieniać swoją formę. W przypadku mechaniki oznacza to, że w układzie odizolowanym suma energii kinetycznej i potencjalnej jest stała.
Podstawowe pojęcia
- Układ odizolowany: układ ciał, na który nie działają żadne siły zewnętrzne (np. tarcie czy opór powietrza). W rzeczywistości taki układ nie istnieje, ale dla uproszczenia wielu problemów fizycznych można założyć, że na niego nic nie oddziałuje.
- Energia kinetyczna: energia ruchu.
- Energia potencjalna: energia położenia.
- Energia mechaniczna: suma energii kinetycznej i potencjalnej.
Zasada zachowania energii mechanicznej
Wzór ten oznacza, że energia całkowita w dowolnym punkcie ruchu jest taka sama jak w innym. Jeśli ciało traci energię potencjalną, to zyskuje dokładnie tyle samo energii kinetycznej.
$$E_p + E_k = const$$
lub $$E_{p1} + E_{k1} = E_{p2} + E_{k2}$$
Przykład:
Dziecko o masie 20 kg zjeżdża z górki na sankach o wysokości 5 metrów, startując ze spoczynku. Z jaką prędkością dojedzie do jej podnóża, jeśli pominiemy siłę tarcia?
Rozwiązanie:Zgodnie z zasadą zachowania energii, energia potencjalna na szczycie zamieni się w energię kinetyczną na dole. $$E_{p(góra)} = E_{k(dół)}$$ $$m⋅g⋅h=\frac{1}{2}⋅v^2$$
Obie strony równania dzielimy przez masę (m): $$g⋅h=\frac{1}{2}v^2$$
Przekształcamy wzór, aby obliczyć prędkość (v):$$v=\sqrt{2gh}$$
Podstawiamy dane: $$v=\sqrt{2⋅9,81\frac{m}{s^2}⋅5m}=\sqrt{98,1}\approx9,9\frac{m}{s}$$
Prawo powszechnego ciążenia mówi, że każde dwa ciała we Wszechświecie przyciągają się wzajemnie siłą, która zależy od ich mas i odległości między nimi. To właśnie dzięki tej sile Ziemia krąży wokół Słońca, a Księżyc wokół Ziemi.
Podstawowe pojęcia
- Siła grawitacji: siła, z jaką ciała wzajemnie się przyciągają. Jest zawsze siłą przyciągającą i działa wzdłuż linii łączącej środki mas ciał.
- Masa: masy dwóch oddziałujących ciał. Im większe masy, tym większa siła przyciągania.
- Odległość: odległość między środkami mas tych ciał. Siła grawitacji maleje bardzo szybko wraz ze wzrostem odległości (proporcjonalnie do kwadratu odległości).
- Stała grawitacji: stała wartość, która jest taka sama w całym Wszechświecie.
Siła grawitacji
Ten wzór pozwala obliczyć siłę przyciągania między dwoma ciałami, znając ich masy oraz odległość między ich środkami.
$$F_g=G⋅\frac{m_1⋅m_2}{r^2}$$
Przykład:
Z jaką siłą przyciągają się dwa ciała, z których każde ma masę 1 kg, a ich środki są odległe o 1 metr?
Rozwiązanie:$$F_g=6,67⋅10_{-11}⋅\frac{1kg⋅1kg}{(1m)^2}=6,67⋅10^{-11}N$$
Prędkości kosmiczne to minimalne prędkości początkowe, jakie musi osiągnąć ciało, aby pokonać siłę grawitacji i pozostać w kosmosie.
Podstawowe pojęcia
- Prędkość orbitalna (pierwsza prędkość kosmiczna): minimalna prędkość, jaką trzeba nadać ciału, aby weszło na kołową orbitę wokół planety, nie spadając na nią. Ciało wpadnie w stały ruch po okręgu wokół planety.
- Prędkość ucieczki (druga prędkość kosmiczna): minimalna prędkość, jaką trzeba nadać ciału, aby na zawsze opuściło pole grawitacyjne planety, nie wracając już na nią.
- Wzory na prędkości kosmiczne: zależą od masy planety oraz jej promienia. Im większa masa planety, tym większe prędkości są potrzebne.
Pierwsza prędkość kosmiczna
Wzór ten pozwala obliczyć minimalną prędkość potrzebną, aby wejść na orbitę wokół planety. G to stała grawitacji.
$$v_I=\sqrt{\frac{GM}{R}}$$
Przykład:
Jaką prędkość musi osiągnąć sonda kosmiczna, aby wejść na niską orbitę wokół Marsa, którego masa wynosi 6,42⋅$10^{23}$ kg, a promień 3390 km?
Rozwiązanie:Przekształcamy promień na metry (3390km=3390000m). Następnie podstawiamy dane do wzoru: $$v_I=\sqrt{\frac{6,67⋅10^{-11}⋅6,42⋅10^{23}}{3,39⋅10^6}}\approx\sqrt{1,26⋅10^7}\approx3550\frac{m}{s}\approx3,55\frac{km}{s}$$
Druga prędkość kosmiczna
Wzór ten pozwala obliczyć minimalną prędkość ucieczki z pola grawitacyjnego planety. Jest ona $\sqrt2$ razy większa od pierwszej prędkości kosmicznej.
$$v_{II}=\sqrt{\frac{2GM}{R}}$$
Przykład:
Z jaką prędkością rakieta musi wystartować z powierzchni Marsa, aby na zawsze opuścić jego pole grawitacyjne? Wykorzystajmy dane z poprzedniego pytania.
Rozwiązanie:$$v_{II}=\sqrt{\frac{2⋅6,67⋅10^{-11}⋅6,42⋅10^{23}}{3,39⋅10^6}}\approx\sqrt{2,52⋅10^7}\approx5020\frac{m}{s}\approx5,02\frac{km}{s}$$
Alternatywnie, możemy skorzystać z zależności między prędkościami:$$v_{II}=v_I⋅\sqrt{2}=3,55\frac{km}{s}⋅1,414\approx5,02\frac{km}{s}$$
Prawa Keplera opisują ruch ciał niebieskich, takich jak planety, wokół gwiazd. Uprzedziły one Prawo powszechnego ciążenia Newtona i są kluczowe dla zrozumienia dynamiki Układu Słonecznego.
I Prawo Keplera (Prawo elips)
Każda planeta porusza się po elipsie, a Słońce znajduje się w jednym z jej ognisk. Oznacza to, że odległość planety od Słońca nie jest stała. W punkcie najbliższym Słońcu (peryhelium) jest mniejsza, a w najdalszym (aphelium) jest większa.
Podstawowe pojęcia
- Elipsa: zamknięta krzywa, która przypomina spłaszczony okrąg.
- Ognisko: punkt wewnątrz elipsy. Suma odległości z dowolnego punktu na elipsie do obu ognisk jest stała.
II Prawo Keplera (Prawo pól)
Promień wodzący (linia łącząca Słońce z planetą) zakreśla równe pola w równych odstępach czasu. Prawo to oznacza, że prędkość planety nie jest stała. Gdy planeta jest bliżej Słońca, porusza się szybciej, a gdy jest dalej – wolniej.
Podstawowe pojęcia
- Promień wodzący: wyimaginowana linia łącząca Słońce z planetą.
- Peryhelium: punkt na orbicie, w którym planeta jest najbliżej Słońca (największa prędkość).
- Aphelium: punkt na orbicie, w którym planeta jest najdalej od Słońca (najmniejsza prędkość).
III Prawo Keplera (Prawo okresów)
Stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu jej średniej odległości od Słońca jest stały dla wszystkich planet.
Podstawowe pojęcia
- Okres obiegu: czas potrzebny planecie na wykonanie jednego pełnego obiegu wokół Słońca.
- Średnia odległość: średnia odległość planety od Słońca.
III Prawo Kelpera
Wzór ten pozwala porównać ruch dwóch planet wokół tej samej gwiazdy. Jest on stały dla każdej planety krążącej wokół tego samego ciała centralnego.
$$\frac{T^2}{a^3}=const$$
Przykład:
Okres obiegu Merkurego wynosi 88 dni, a jego średnia odległość od Słońca to 58 mln km. Jaka jest średnia odległość Ziemi od Słońca, jeśli jej okres obiegu wynosi 365 dni?
Rozwiązanie: Korzystamy ze stałej proporcji:$$\frac{T_{Ziemi}^2}{a_{Ziemi}^2}=\frac{T_{Merkurego}^2}{a_{Merkurego}^3}$$ $$a_{Ziemi}^3=a_{Merkurego}^3⋅\frac{T_{Ziemi}^2}{T_{Merkurego}^2}$$ $$a_{Ziemi}=\sqrt[3]{(58 mln km)^3⋅\frac{(365 dni)^2}{88 dni}^2}=149\, mln\, km$$
Wszystka materia wokół nas składa się z atomów i cząsteczek. Ich budowa i ruch decydują o właściwościach ciał stałych, cieczy i gazów, a także o zjawiskach, które opisuje termodynamika.
Podstawowe pojęcia
- Atom: podstawowy składnik materii, który składa się z jądra (protonów i neutronów) oraz elektronów krążących wokół niego.
- Cząsteczka: najmniejsza część substancji, która zachowuje wszystkie jej właściwości chemiczne. Składa się z co najmniej dwóch połączonych atomów.
- Ruch cieplny (drgania): atomy i cząsteczki w każdym ciele są w nieustannym, chaotycznym ruchu. Rodzaj tego ruchu zależy od stanu skupienia:
W ciałach stałych cząsteczki drgają wokół ustalonych położeń w sieci krystalicznej.
W cieczach cząsteczki mogą przemieszczać się względem siebie, ale wciąż oddziałują ze sobą.
W gazach cząsteczki poruszają się swobodnie, z dużą prędkością i w dużych odległościach od siebie
Stany skupienia materii
Materia występuje w trzech podstawowych stanach: stałym, ciekłym i gazowym. Różnią się one od siebie siłami oddziaływań międzycząsteczkowych oraz swobodą ruchu cząsteczek.
- Ciało stałe: Cząsteczki są ściśle upakowane i mocno oddziałują ze sobą. Mogą jedynie drgać wokół stałych położeń. Dlatego ciała stałe mają stały kształt i objętość.
- Ciało ciekłe: Cząsteczki oddziałują ze sobą, ale słabiej niż w ciałach stałych. Mogą przemieszczać się względem siebie, co pozwala cieczom na przyjmowanie kształtu naczynia, w którym się znajdują. Mają stałą objętość.
- Gaz: Cząsteczki są od siebie daleko i poruszają się swobodnie, zderzając się ze sobą i ze ściankami naczynia. Oddziaływania są pomijalnie małe. Gazy nie mają stałego kształtu ani objętości – rozprężają się, wypełniając całą dostępną przestrzeń.
Zmiany stanów skupienia
Zmiany stanów skupienia zachodzą pod wpływem dostarczania lub odbierania energii (zazwyczaj w postaci ciepła).
- Topnienie: Przejście ze stanu stałego w ciekły (np. lód w wodę). Zachodzi w stałej temperaturze (temperaturze topnienia), a dostarczane ciepło zużywane jest na zerwanie wiązań między cząsteczkami.
- Krzepnięcie: Przejście ze stanu ciekłego w stały (np. woda w lód). Zachodzi w tej samej temperaturze co topnienie, a energia jest oddawana do otoczenia.
- Parowanie: Przejście ze stanu ciekłego w gazowy (np. woda w parę). Może zachodzić w dowolnej temperaturze.
- Wrzenie: Gwałtowne parowanie cieczy w całej jej objętości. Zachodzi w stałej temperaturze (temperaturze wrzenia), a dostarczane ciepło zużywane jest na zmianę stanu.
- Skraplanie (kondensacja): Przejście ze stanu gazowego w ciekły.
- Sublimacja: Bezpośrednie przejście ze stanu stałego w gazowy (np. suchy lód - dwutlenek węgla).
- Resublimacja: Bezpośrednie przejście ze stanu gazowego w stały (np. powstawanie szronu).
Ciepło potrzebne do topnienia/krzepnięcia
Wzór ten pozwala obliczyć ilość ciepła, jaką trzeba dostarczyć, aby stopić masę substancji.
$$Q_t=m⋅L_t$$
Przykład:
Ile ciepła potrzeba, aby stopić 1 kg lodu, jeśli ciepło topnienia lodu wynosi 334000J/kg?
Rozwiązanie:$$Q_t=1kg⋅334000\frac{J}{kg}=334000J$$
Ciepło potrzebne do parowania/skraplania
Wzór ten pozwala obliczyć ilość ciepła, jaką trzeba dostarczyć, aby odparować masę substancji.
$$Q_p=m⋅L_p$$
Przykład:
Ile ciepła potrzeba, aby odparować 1 kg wody, jeśli ciepło parowania wody wynosi $2,26⋅10^6\frac{J}{kg}$?
Rozwiązanie:$$Q_p=1kg⋅2,26⋅10^6\frac{J}{kg}=2,26⋅10^6J$$
Gęstość
Gęstość to miara tego, jak "upakowana" jest materia w danym ciele. Mówi nam o stosunku masy ciała do zajmowanej przez niego objętości. Na przykład, 1 kilogram piór zajmuje znacznie więcej miejsca niż 1 kilogram stali, ponieważ stal ma większą gęstość. Gęstość jest cechą charakterystyczną dla danej substancji.
Podstawowe pojęcia
- Masa: ilość materii w ciele.
- Objętość: przestrzeń zajmowana przez ciało.
Gęstość
Wzór ten pozwala obliczyć gęstość substancji, dzieląc jej masę przez objętość.
$$d=\frac{m}{V}$$
Przykład:
Sześcian o boku 10 cm ma masę 2,7 kg. Jaka jest gęstość materiału, z którego jest wykonany?
Rozwiązanie:Najpierw obliczamy objętość sześcianu, a następnie dzielimy masę przez objętość. Pamiętaj, aby zamienić jednostki na metry. $$a=10cm=0,1m$$ $$V=a^3=(0,1m)^3=0,001m^3$$ $$d=\frac{2,7kg}{0,001 m^3}=2700\frac{kg}{m^3}$$
Ciśnienie
Ciśnienie to wartość, która opisuje, z jaką siłą ciało działa na jednostkę powierzchni. Jest to bardzo użyteczne pojęcie, ponieważ ta sama siła może wywołać różne skutki w zależności od powierzchni, na którą działa. Z tego powodu gwoździe mają ostre końce.
Podstawowe pojęcia
- Siła nacisku: siła działająca prostopadle do powierzchni.
- Powierzchnia: pole powierzchni, na którą działa siła.
Ciśnienie
Wzór ten pozwala obliczyć ciśnienie, dzieląc siłę nacisku przez powierzchnię, na którą ta siła działa.
$$ρ=\frac{F}{S}$$
Przykład:
Człowiek o masie 70 kg stoi na podłodze. Jego buty mają łączną powierzchnię 0,02 m². Jakie ciśnienie wywiera na podłogę?
Rozwiązanie:Najpierw musimy obliczyć siłę, z jaką człowiek naciska na podłogę (jest to jego ciężar): $$F=m⋅g=70kg⋅9,81\frac{m}{s^2}\approx687N$$ Następnie dzielimy siłę przez powierzchnię: $$p=\frac{687N}{0,02m^2}=34350Pa$$
Zjawisko rozszerzalności cieplnej polega na tym, że gdy materia jest ogrzewana, jej objętość lub długość zwiększa się. Dzieje się tak, ponieważ wzrasta energia kinetyczna cząsteczek, przez co zwiększają się ich drgania i odległości między nimi. Rozszerzalność jest różna dla każdego stanu skupienia.
Rozszerzalność cieplna ciał stałych
Ciała stałe rozszerzają się w bardzo niewielkim stopniu. Wyróżniamy rozszerzalność liniową (zmiana długości) i objętościową (zmiana objętości).
Podstawowe pojęcia
- Współczynnik rozszerzalności liniowej (α): wartość charakterystyczna dla danej substancji stałej, która określa, jak zmienia się jej długość pod wpływem zmiany temperatury.
- Współczynnik rozszerzalności objętościowej (β): określa, jak zmienia się objętość ciała stałego. Wartość $β\approx3α$.
Rozszerzalność liniowa
Wzór ten pozwala obliczyć, o ile zmieni się długość pręta po zmianie temperatury.
$$ΔL=L_0⋅α⋅ΔT$$
Przykład:
Stalowy pręt o długości 10 m został ogrzany o 20°C. O ile wydłużył się pręt, jeśli współczynnik rozszerzalności liniowej stali wynosi $1,2⋅10^{-5}\;\frac{1}{°C}$
Rozwiązanie:$$ΔL=10m⋅1,2⋅10^{-5}\;\frac{1}{°C}⋅20\;°C=0,0024m=2,4mm$$
Rozszerzalność cieplna cieczy
Ciecze rozszerzają się bardziej niż ciała stałe, ale w różnym stopniu. Wykorzystuje się to w termometrach cieczowych, w których zmiana objętości cieczy jest proporcjonalna do zmiany temperatury. Wyjątkiem jest woda, która ma największą gęstość w temperaturze 4°C.
Podstawowe pojęcia
- Współczynnik rozszerzalności objętościowej (β): wartość charakterystyczna dla danej cieczy.
Rozszerzalność objętościowa
Wzór ten pozwala obliczyć, o ile zmieni się objętość cieczy po zmianie temperatury.
$$ΔV=V_0⋅β⋅ΔT$$
Przykład:
Ile zmieni się objętość 2 litrów alkoholu etylowego, jeśli ogrzejemy go od 20°C do 40°C? Współczynnik rozszerzalności objętościowej alkoholu wynosi $1,1⋅10^{-4}\;\frac{1}{°C}$
Rozwiązanie:$$ΔV=2l⋅1,1⋅10^{-4}\;\frac{1}{°C}⋅20\;°C=0,0044l=4,4ml$$
Rozszerzalność cieplna gazów
Gazy rozszerzają się znacznie bardziej niż ciecze i ciała stałe, a ich rozszerzalność jest prawie jednakowa dla wszystkich gazów. Wzrost objętości gazu jest wprost proporcjonalny do wzrostu jego temperatury, jeśli ciśnienie pozostaje stałe./p>
Podstawowe pojęcia
- Prawo Charles'a: opisujące zależność między objętością a temperaturą gazu.
Rozszerzalność gazów (prawo Charles'a)
Wzór ten pozwala obliczyć nową objętość lub temperaturę gazu, gdy zmienia się jego stan. Pamiętaj, aby temperaturę wstawiać w skali Kelvina.
$$\frac{V_1}{T_1}=\frac{V_2}{T_2}$$
Przykład:
Balon o objętości $1 m^3$ ma temperaturę 20°C. Do jakiej temperatury musimy go ogrzać, aby jego objętość wzrosła do $1,2 m^3$?
Rozwiązanie: Najpierw zmieniamy temperaturę na kelwiny: $$T_1=20°C+273,15=293,15K$$ potem przekształcamy wzór do $T_2$: $$T_2=\frac{V_2⋅T_1}{V_1}$$ podstawiamy dane do wzoru: $$T_2=\frac{1,2m^3⋅293,15K}{1m^3}\approx351,78K$$ i na koniec wracamy do stopni celsjusza $$T_2=351,78K-273,15\approx78,63°C$$
Temperatura to miara stopnia nagrzania ciała. Na poziomie mikroskopowym jest to miara średniej energii kinetycznej chaotycznego ruchu cząsteczek. Im wyższa temperatura, tym szybciej poruszają się cząsteczki.
Skale temperatur
Istnieją różne skale, które pozwalają zmierzyć temperaturę. Najczęściej używane to skala Celsjusza, Fahrenheita i Kelvina.
Skala Celsjusza (°C)
Jest to skala, którą najczęściej posługujemy się na co dzień.
- 0°C to temperatura topnienia lodu pod normalnym ciśnieniem.
- 100°C to temperatura wrzenia wody pod normalnym ciśnieniem.
Skala Kelvina (K)
Jest to absolutna skala temperatur, kluczowa w fizyce i chemii. Jej zerem jest zero absolutne, czyli najniższa możliwa temperatura, w której ustaje wszelki ruch cząsteczek.
- 0 K = −273,15°C.
- 1 K odpowiada zmianie temperatury o 1°C.
Skala Fahrenheita (°F)
Jest używana głównie w Stanach Zjednoczonych.
- 32°F to temperatura topnienia lodu.
- 212°F to temperatura wrzenia wody.
Konwersja z Celsjusza na Kelwiny
$$T_K=T_C+273,15$$
Przykład:
Jaka jest temperatura 25°C w skali Kelvina?
Rozwiązanie:$$T_K=25+273,15=298,15K$$
Konwersja z Fahrenheita na Celsjusza
$$T_C=\frac{5}{9}(T_F-32)$$
Przykład:
Jaka jest temperatura 68°F w skali Celsjusza?
Rozwiązanie:$$T_C=\frac{5}{9}(68-32)=\frac{5}{9}⋅36=20°C$$
Konwersja z Fahrenheita na Kelwiny
$$T_K=(T_F-32)⋅\frac{5}{9}=273,15$$
Przykład:
Jaka jest temperatura 68°F w skali Kelvina?
Rozwiązanie:$$T_K=(68-32)⋅\frac{5}{9}+273,15=36⋅\frac{5}{9}+273,15=20+273,15=293,15K$$
Energia wewnętrzna
Energia wewnętrzna to suma całkowitej energii kinetycznej i potencjalnej wszystkich cząsteczek w danym ciele. Innymi słowy, jest to energia, która "drzemie" wewnątrz materii. Zmiana energii wewnętrznej jest związana ze zmianą temperatury ciała lub zmianą jego stanu skupienia.
Podstawowe pojęcia
- Energia kinetyczna cząsteczek: związana z ich chaotycznym ruchem. Rośnie wraz z temperaturą.
- Energia potencjalna cząsteczek: związana z odległościami i oddziaływaniami między cząsteczkami. Zmienia się podczas przemian fazowych (np. topnienia, wrzenia).
Ciepło
Ciepło to forma przekazywania energii wewnętrznej. Przekazywanie energii następuje zawsze od ciała o wyższej temperaturze do ciała o niższej temperaturze. Jest to proces, który zachodzi spontanicznie, aż do momentu, w którym temperatury się wyrównają.
Podstawowe pojęcia
- Ciepło właściwe: ilość ciepła, jaką trzeba dostarczyć 1 kg danej substancji, aby podgrzać ją o 1°C. To miara "oporności" substancji na zmianę temperatury.
- Pojemność cieplna: ilość ciepła, jaką trzeba dostarczyć, aby podgrzać całe ciało o 1°C.
Ciepło właściwe
Wzór ten pozwala obliczyć ilość ciepła, jaką trzeba dostarczyć, aby podgrzać masę substancji o daną temperaturę.
$$Q=m⋅c_w⋅ΔT$$
Przykład:
Ile ciepła trzeba dostarczyć 2 kg wody, aby podgrzać ją od 20°C do 40°C? (Ciepło właściwe wody wynosi $4200\frac{J}{kg⋅°C}$).
Rozwiązanie:$$Q=2kg⋅4200\frac{J}{kg⋅°C}⋅20°C=168000J=168kJ$$
Zerowa zasada termodynamiki
Ta zasada mówi, że jeśli dwa ciała są w równowadze termicznej z trzecim ciałem, to są one również w równowadze termicznej między sobą. Prościej mówiąc, jeśli termometr wskazuje, że twój kubek kawy i dzbanek herbaty mają tę samą temperaturę, to znaczy, że kubek i dzbanek również mają taką samą temperaturę. To jest podstawa, na której działają termometry.
Podstawowe pojęcia
- Równowaga termiczna: stan, w którym dwa ciała mają taką samą temperaturę i nie następuje przepływ ciepła między nimi.
Pierwsza zasada termodynamiki
Energia wewnętrzna układu może zmienić się tylko wtedy, gdy układ wymieni energię z otoczeniem, czyli gdy zostanie dostarczona praca lub ciepło. Energia nie ginie, tylko zmienia formę. Przykładowo, jeśli ogrzewasz garnek z wodą, dostarczasz mu ciepło, które zwiększa jego energię wewnętrzną.
Podstawowe pojęcia
- Energia wewnętrzna: suma energii kinetycznej i potencjalnej cząsteczek w układzie.
- Ciepło: energia dostarczona do układu lub oddana przez niego.
- Praca: energia wymieniona między układem a otoczeniem, związana ze zmianą objętości (np. gaz rozprężający się i pchający tłok).
Energia wewnętrzna
Zmiana energii wewnętrznej jest równa sumie ciepła dostarczonego do układu i pracy wykonanej nad układem. Pamiętaj o znakach! Jeśli ciepło jest dostarczane, Q>0. Jeśli układ wykonuje pracę, W<0.
$$ΔU=Q+W$$
Przykład:
Do gazu dostarczono 500 J ciepła. Gaz rozprężył się i wykonał pracę 200 J. Jak zmieniła się energia wewnętrzna gazu?
Rozwiązanie:$$ΔU=500J+(-200J)=300J$$
Druga zasada termodynamiki
Ta zasada dotyczy kierunku, w jakim zachodzą procesy w przyrodzie. Mówi, że ciepło zawsze spontanicznie przepływa od ciała cieplejszego do ciała zimniejszego. Nigdy nie zaobserwujesz, żeby zimny lód nagle się ochłodził, a otoczenie samo z siebie się nagrzało. Innym ujęciem tej zasady jest to, że całkowita entropia (miara nieuporządkowania) w układzie zamkniętym nigdy nie maleje.
Podstawowe pojęcia
- Entropia: miara nieuporządkowania, chaosu w układzie. W naturalnych procesach entropia zawsze rośnie.
Energia wewnętrzna
Ten zapis symbolizuje, że ciepło samoczynnie przepływa tylko w jednym kierunku: od obszaru o wyższej temperaturze do obszaru o niższej temperaturze.
$$Q_{ciepłe}→Q_{zimne}$$
Trzecia zasada termodynamiki
Gdy temperatura układu dąży do zera bezwzględnego (0 K), entropia układu dąży do stałej, minimalnej wartości. Jeśli jest to ciało idealnie uporządkowane (kryształ), jego entropia w temperaturze 0 K wynosi zero.
Podstawowe pojęcia
- Entropia: miara nieuporządkowania w układzie.
- Zero bezwzględne: najniższa możliwa temperatura, w której ustaje wszelki ruch cząsteczek.
Wniosek: Osiągnięcie temperatury zera absolutnego jest niemożliwe. Im bardziej zbliżamy się do tej temperatury, tym trudniej jest obniżyć ją jeszcze bardziej.
Silnik cieplny to urządzenie, które zamienia energię cieplną w pracę mechaniczną. Aby to osiągnąć, silnik musi pracować między dwoma zbiornikami ciepła o różnych temperaturach: cieplejszym (źródło ciepła) i zimniejszym (chłodnica). Silnik pobiera ciepło ze źródła, część zamienia na pracę, a resztę oddaje do chłodnicy.
Podstawowe pojęcia
- Źródło ciepła: zbiornik o wyższej temperaturze, z którego pobierane jest ciepło.
- Chłodnica: zbiornik o niższej temperaturze, do którego oddawane jest ciepło.
- Praca: użyteczna praca wykonana przez silnik. Jest to różnica między ciepłem pobranym a ciepłem oddanym.
- Sprawność: miara efektywności silnika, czyli stosunek uzyskanej pracy do pobranego ciepła.
Wzory
Sprawność mówi nam, jaki procent pobranego ciepła został zamieniony na użyteczną pracę. Im wyższa sprawność, tym silnik jest bardziej efektywny. Sprawność nigdy nie wynosi 100%, co jest konsekwencją drugiej zasady termodynamiki.
To teoretyczna, maksymalna sprawność, jaką może osiągnąć silnik pracujący między dwoma temperaturami. Nie da się jej przekroczyć. Temperatury w tym wzorze muszą być podane w Kelwinach
Przykład:
Silnik pobrał ze źródła ciepło o wartości 1000 J i wykonał pracę 300 J. Ile ciepła oddał do chłodnicy i jaka jest jego sprawność?
Rozwiązanie:
Obliczamy ciepło oddane do chłodnicy.$$Q_2=Q_1-W=1000J-300J-700J$$ Obliczamy sprawność.$$η=\frac{W}{Q_1}=\frac{300J}{1000J}=0,3=30\%$$
Wszystko, co nas otacza, składa się z atomów, a te z kolei zawierają cząstki obdarzone ładunkiem elektrycznym: protony (ładunek dodatni) i elektrony (ładunek ujemny). Ładunek elektryczny jest jedną z fundamentalnych właściwości materii.
Ładunki elektryczne
Ładunki elektryczne mogą być dodatnie lub ujemne. Ładunki o tym samym znaku odpychają się, a ładunki o przeciwnych znakach przyciągają się. Zjawisko to nazywamy oddziaływaniem elektrostatycznym. Ładunek elektryczny jest skwantowany, co oznacza, że zawsze występuje w postaci całkowitej wielokrotności ładunku elementarnego (e), czyli ładunku jednego elektronu lub protonu.
Podstawowe pojęcia
- Ładunek elektryczny: właściwość cząstek, która powoduje oddziaływania elektryczne. Jednostką ładunku jest kulomb.
- Ładunek elementarny: najmniejszy, podstawowy ładunek, jaki może występować. Jego wartość to $e\approx1,602⋅10^{-19}C.$
Prawo Coulomba
Prawo Coulomba opisuje siłę oddziaływania elektrostatycznego między dwoma ładunkami punktowymi. Mówi, że siła ta jest wprost proporcjonalna do iloczynu wartości ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi.
Prawo Coulomba
Wzór ten pozwala obliczyć siłę przyciągania lub odpychania między dwoma ładunkami oddalonymi od siebie o odległość. Stała k (stała Coulomba) wynosi $k\approx9⋅10^9\frac{N⋅m^2}{C^2}$.
$$F=k\frac{|q_1⋅q_2|}{r^2}$$
Przykład:
Z jaką siłą przyciągają się dwa ładunki, $q_1=2C$ i $q_2=-3C$, oddalone od siebie o 3 metry?
Rozwiązanie:$$F=9⋅10^9⋅\frac{|2C⋅(-3)C|}{(3m)^2}=9⋅10^9⋅\frac{6}{9}=6⋅10^9N$$
Pole elektryczne to obszar przestrzeni, w którym na umieszczone ładunki działają siły elektryczne. Samo pole jest niewidoczne, ale jego istnienie możemy zaobserwować, gdy inne ładunki w jego zasięgu zaczynają się poruszać. Każdy ładunek, czy to dodatni, czy ujemny, wytwarza wokół siebie pole elektryczne.
Podstawowe pojęcia
- Linie pola elektrycznego: umowne linie, które pokazują kierunek i siłę pola. Linie zawsze zaczynają się na ładunkach dodatnich i kończą na ujemnych. Im linie są gęstsze, tym silniejsze jest pole w danym miejscu.
- Natężenie pola elektrycznego: wielkość wektorowa, która określa siłę działającą na jednostkowy ładunek dodatni umieszczony w danym punkcie pola.
Natężenie pola elektrycznego
Wzór ten pozwala obliczyć natężenie pola elektrycznego w danym punkcie, dzieląc siłę, która działa na umieszczony tam ładunek próbny, przez wartość tego ładunku. Jednostką natężenia jest niuton na kulomb.
$$E=\frac{F}{q}$$
Przykład:
Na ładunek $q=2⋅10^{-6}C$ umieszczony w polu elektrycznym działa siła 4 N. Jakie jest natężenie tego pola?
Rozwiązanie:$$E=\frac{4N}{2⋅10^{-6}C}=2⋅10^6\frac{N}{C}$$
Siła działającą w polu elektrycznym
Wzór ten jest przekształceniem poprzedniego i pozwala obliczyć siłę, jaka będzie działać na ładunek umieszczony w polu o znanym natężeniu.
$$F=q⋅E$$
Przykład:
Jakiej siły doświadczy elektron (ładunek $e\approx1,6⋅10^{-19}C$ umieszczony w polu o natężeniu $20\frac{N}{C}$?
Rozwiązanie:$$1,6⋅10^{-19}C⋅20\frac{N}{C}=3,2⋅10^{-18}N$$
Potencjał elektryczny
Potencjał elektryczny (V) to wartość, która określa zdolność pola elektrycznego do wykonania pracy. Mówi nam, ile energii potencjalnej ma jednostkowy ładunek w danym punkcie pola. Ładunki, tak jak ciała na górce, mają tendencję do przemieszczania się z obszaru o wyższym potencjale do obszaru o niższym potencjale.
Podstawowe pojęcia
- Potencjał elektryczny: energia potencjalna jednostkowego ładunku w polu elektrycznym.
- Energia potencjalna: energia, jaką ma ładunek dzięki swojemu położeniu w polu.
- Ładunek: wartość ładunku, który znajduje się w polu.
Napięcie elektryczne
Napięcie elektryczne to różnica potencjałów między dwoma punktami w polu elektrycznym. To właśnie napięcie jest "siłą napędową", która powoduje przepływ prądu. Im większe napięcie, tym więcej pracy może wykonać pole elektryczne, przesuwając ładunek między dwoma punktami.
Podstawowe pojęcia
- Napięcie: różnica potencjałów, mierzona w woltach.
- Praca: praca wykonana przez pole elektryczne na przesunięcie ładunku.
- Ładunek: wartość ładunku, który jest przesuwany.
Potencjał elektryczny
Wzór ten pozwala obliczyć potencjał w danym punkcie pola, dzieląc energię potencjalną, jaką ma ładunek, przez wartość tego ładunku.
$$V=\frac{E_p}{q}$$
Przykład:
Ładunek 2C umieszczony w pewnym punkcie pola ma energię potencjalną 10J. Jaki jest potencjał w tym punkcie?
Rozwiązanie:$$V=\frac{10J}{2C}=5V$$
Napięcie elektryczne
Wzór ten pozwala obliczyć napięcie, dzieląc pracę wykonaną przez pole na przesunięcie ładunku, przez wartość tego ładunku.
$$U=\frac{W}{q}$$
Przykład:
Aby przesunąć ładunek 4C między dwoma punktami pola, pole elektryczne wykonało pracę 24J. Jakie jest napięcie między tymi punktami?
Rozwiązanie:$$U=\frac{24J}{4C}=6V$$
Kondensator to urządzenie, które służy do gromadzenia ładunku elektrycznego, a co za tym idzie, również energii. Działa na zasadzie oddziaływania elektrostatycznego. Składa się z dwóch przewodzących płytek (okładek) oddzielonych izolatorem (dielektrykiem).
Podstawowe pojęcia
- Pojemność elektryczna: wielkość, która mówi nam, ile ładunku elektrycznego kondensator może zgromadzić przy danym napięciu. Jest to cecha charakterystyczna kondensatora. Jednostką pojemności jest farad [F].
- Ładunek: ładunek zgromadzony na okładkach kondensatora.
- Napięcie: różnica potencjałów między okładkami kondensatora.
Pojemność elektryczna
Wzór ten pozwala obliczyć pojemność kondensatora, dzieląc ładunek zgromadzony na jego okładkach przez napięcie między nimi.
$$C=\frac{q}{U}$$
Przykład:
Na okładkach kondensatora zgromadzono ładunek 0,01 C przy napięciu 5 V. Jaka jest jego pojemność?
Rozwiązanie:$$C=\frac{0,01C}{5V}=0,002F=2mF$$
Energia zgromadzona w kondensatorze
Wzór ten pozwala obliczyć energię, jaką zgromadził kondensator. Zauważ, że energia jest proporcjonalna do kwadratu napięcia.
$$E=\frac{1}{2}C⋅U^2$$
Przykład:
Ile energii zgromadził kondensator o pojemności 2 mF, naładowany do napięcia 5 V?
Rozwiązanie:$$E=\frac{1}{2}⋅0,002F⋅(5V)^2=\frac{1}{2}⋅0,002⋅25=0,025J$$
Zastosowania kondensatorów
Kondensatory są używane w wielu urządzeniach elektronicznych, np.:
- Lampy błyskowe: kondensator gromadzi energię, a następnie oddaje ją bardzo szybko, tworząc intensywny błysk światła.
- Filtry w zasilaczach: kondensatory wygładzają napięcie, zapewniając stały i stabilny prąd.
- Układy rozruchu silników: silny impuls prądu z kondensatora pomaga w uruchomieniu silnika.
Prąd elektryczny to uporządkowany ruch ładunków elektrycznych. Wyróżniamy dwa podstawowe rodzaje prądu, które różnią się kierunkiem i wartością.
Prąd stały
W prądzie stałym elektrony płyną zawsze w jednym kierunku. Wartość napięcia i natężenia prądu są stałe w czasie. Taki prąd wytwarzają na przykład baterie, akumulatory czy panele słoneczne.
Prąd przemienny
W prądzie przemiennym kierunek przepływu elektronów cyklicznie się zmienia, na przykład 50 razy na sekundę. Wartość napięcia i natężenia również zmienia się sinusoidalnie w czasie. Jest to prąd, który płynie w gniazdkach elektrycznych w naszych domach.
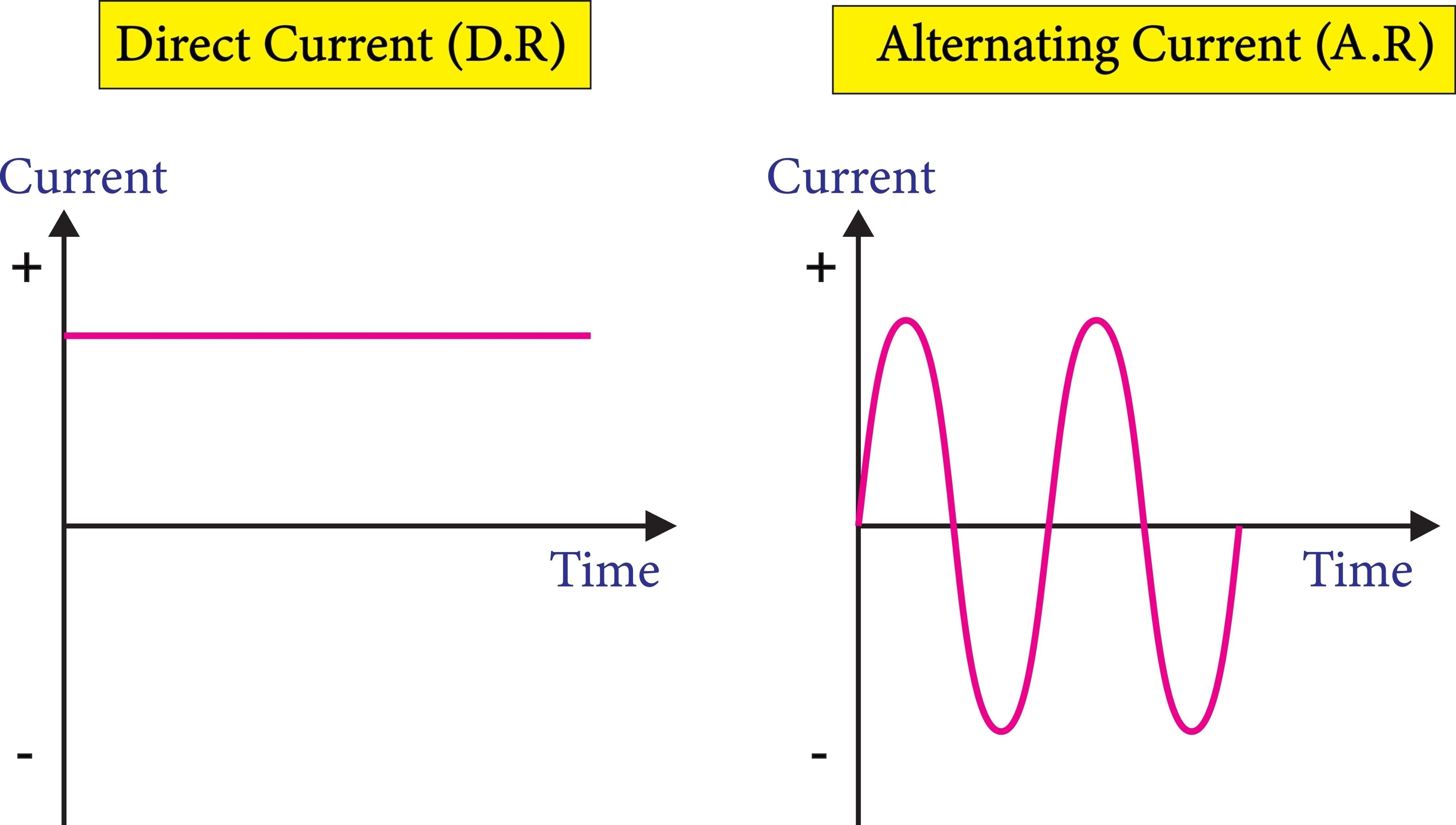
Porównanie i przykłady
- Prąd stały (DC):
Źródła: Baterie, akumulatory, zasilacze.
Zastosowania: Urządzenia elektroniczne (telefony, komputery), samochody (akumulatory), systemy solarne.
- Prąd przemienny (AC):
Źródła: Gniazdka elektryczne, generatory w elektrowniach.
Zastosowania: Oświetlenie domowe, silniki elektryczne, urządzenia RTV i AGD (pralka, lodówka).
Prawo Ohma opisuje prostą, ale fundamentalną zależność między napięciem, prądem i oporem w obwodzie elektrycznym. Mówi, że natężenie prądu płynącego przez przewodnik jest wprost proporcjonalne do napięcia między jego końcami i odwrotnie proporcjonalne do oporu tego przewodnika.
Podstawowe pojęcia
- Natężenie prądu: Mówi o tym, jak dużo ładunków przepływa przez przekrój przewodnika w jednostce czasu.
- Napięcie: Różnica potencjałów, która jest "siłą napędową" dla prądu.
- Opór elektryczny: Wielkość, która charakteryzuje właściwości przewodnika i mówi, jak bardzo "przeszkadza" on przepływowi prądu.
Wzór na natężenie prądu:
Wzór ten pozwala obliczyć natężenie prądu, dzieląc napięcie przez opór.
$$I=\frac{U}{R}$$
Przykład:
Jakie jest natężenie prądu w obwodzie, w którym napięcie wynosi 12 V, a opór 6 Ω?
Rozwiązanie:$$I=\frac{12 V}{6 Ω}= 2 A$$
Wzór na opór (przekształcenie prawa Ohma):
Wzór ten pozwala obliczyć opór, dzieląc napięcie przez natężenie prądu.
$$R=\frac{U}{I}$$
Przykład:
Prąd o natężeniu 0,5 A płynie przez opornik, na którym jest napięcie 5 V. Jaki jest opór tego opornika?
Rozwiązanie:$$R=\frac{5 V}{0,5 A}= 10 Ω$$
Wzór na napięcie (przekształcenie prawa Ohma):
Wzór ten pozwala obliczyć napięcie, mnożąc natężenie prądu przez opór.
$$U=\frac{I}{R}$$
Przykład:
Jakie napięcie jest potrzebne, aby przez opornik o oporze 20 Ω płynął prąd o natężeniu 2 A?
Rozwiązanie:$$U=2A⋅20Ω=40V$$
W obwodach elektrycznych często spotykamy się z sytuacją, gdy oporniki są połączone szeregowo lub równolegle. Aby obliczyć opór całego układu, należy zastosować odpowiednie wzory.
Łączenie szeregowe
W łączeniu szeregowym oporniki są połączone jeden za drugim. Prąd płynie kolejno przez każdy z nich. W takim układzie opór całkowity jest sumą oporów poszczególnych oporników.
Wzór na opór zastępczy
W łączeniu szeregowym natężenie prądu jest takie samo w każdym punkcie obwodu, natomiast napięcie rozkłada się na poszczególne oporniki.
$$R_z=R_1+R_2+...+R_n$$
Przykład:
Trzy oporniki o oporach 2 Ω, 3 Ω i 5 Ω połączono szeregowo. Jaki jest opór zastępczy tego układu?
Rozwiązanie:$$R_z=2Ω+3Ω+5Ω=10Ω$$
Łączenie równoległe
W łączeniu równoległym oporniki są połączone "obok siebie", tworząc rozgałęzienia. Prąd, płynąc do rozgałęzienia, dzieli się na mniejsze prądy w każdym oporniku.
Wzór na opór zastępczy
W łączeniu równoległym napięcie (U) na każdym oporniku jest takie samo, natomiast natężenie prądu (I) dzieli się na poszczególne gałęzie. Prąd wybiera "drogę" o mniejszym oporze
$$\frac{1}{R_z}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_n}$$
Przykład:
Dwa oporniki o oporach 2 Ω i 4 Ω połączono równolegle. Jaki jest opór zastępczy tego układu?
Rozwiązanie:$$\frac{1}{R_z}=\frac{1}{2Ω}+\frac{1}{4Ω}=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}$$
Prąd elektryczny wykonuje pracę, przenosząc ładunek elektryczny przez przewodnik pod napięciem. Praca prądu to energia elektryczna przekazywana w czasie przepływu prądu. Moc prądu jest miarą szybkości wykonywania pracy, czyli stosunku energii do czasu. Jednostką pracy i energii jest dżul, a jednostką mocy - wat.
Podstawowe pojęcia
- Ładunek elektryczny: to właściwość materii, która powoduje oddziaływania elektrostatyczne, a jego jednostką jest kulomb.
- Praca: to ilość energii przekazanej przez prąd podczas przepływu ładunku w obwodzie.
- Moc: to szybkość wykonywania pracy przez prąd, czyli ilość energii przekazywanej w jednostce czasu.
Wzór na moc prądu elektrycznego
Moc to iloczyn napięcia i natężenia prądu.
$$P=U⋅I$$
Przykład:
Oblicz moc silnika, jeśli napięcie wynosi 230 V, a natężenie prądu 5 A.
Rozwiązanie:$$P=230V⋅5A=1150W$$
Wzór na pracę prądu elektrycznego
Praca to energia przekazana przez prąd, obliczana jako iloczyn napięcia, natężenia prądu oraz czasu.
$$W=U⋅I⋅t$$
Przykład:
Ile energii zużyje latarka zasilana napięciem 4,5 V przez prąd o natężeniu 0,15 A, gdy działa przez 100 s?
Rozwiązanie:$$W=4,5V⋅0,15A⋅100s=67,5J$$
Wzór na ładunek elektryczny
Ładunek elektryczny przepływający przez przewodnik to iloczyn natężenia prądu i czasu przepływu.
$$Q=I⋅t$$
Przykład:
Oblicz ładunek przepływający przez żarówkę, jeśli prąd ma natężenie 4 A, a czas przepływu wynosi 600 s.
Rozwiązanie:$$Q=4A⋅600s=2400C$$
Pole magnetyczne jest to vectorowa wielkość fizyczna, którą charakteryzuje indukcja magnetyczna B. W polu magnetycznym na poruszające się ładunki działa siła magnetyczna (siła Lorentza). Pole magnetyczne jest podstawowym pojęciem w elektromagnetyzmie oraz kluczowym tematem na maturze rozszerzonej.
Podstawowe pojęcia
- Pole magnetyczne: to obszar, w którym na poruszające się ładunki elektryczne i magnesy działają siły magnetyczne.
- Indukcja magnetyczna: opisuje pole magnetyczne i jest mierzona w teslach./li>
- Linie pola magnetycznego: wychodzą z bieguna północnego magnesu i wchodzą do bieguna południowego.
Wzór na siłę Lorentza działającą na ładunek elektryczny poruszający się w polu magnetycznym
Siła Lorentza jest maksymalna, gdy ruch ładunku jest prostopadły do pola magnetycznego.
$$F=q⋅v⋅B⋅sin0$$
Przykład:
Oblicz wartość siły działającej na ładunek $q=1,6⋅10^{-19}C$ poruszający się z prędkością $v=3⋅10^6 \frac{m}{s}$ prostopadle do pola magnetycznego o indukcji $B=0,01T$
Rozwiązanie:$$F=1,6⋅10^{-19}⋅3⋅10^6⋅0,01=4,8⋅10^{-15}N$$
Wzór na siłę działającą na przewodnik z prądem umieszczony w polu magnetycznym
Siła jest maksymalna gdy przewodnik jest prostopadły do linii pola magnetycznego.
$$F=B⋅I⋅L⋅sin0$$
Przykład:
Przewodnik o długości 0,5 m, przez który płynie prąd 2 A, znajduje się prostopadle do pola o indukcji 0,1 T. Oblicz siłę działającą na przewodnik.
Rozwiązanie:$$F=0,1⋅2⋅0,5=0,1N$$
Wzór na wartość indukcji magnetycznej pola wytwarzanego przez prostoliniowy przewodnik z prądem
$$B=\frac{μ_0⋅I}{2πr}$$
Siła Lorentza to siła działająca na ładunki elektryczne poruszające się w polu magnetycznym, która powoduje ich odchylenie od prostej drogi. Siła elektromotoryczna to napięcie źródła energii elektrycznej, które wykonuje pracę przemieszczenia ładunków w obwodzie elektrycznym. Oba te pojęcia są kluczowe w zrozumieniu działania urządzeń elektrycznych i magnetycznych, a także na maturze rozszerzonej z fizyki.
Podstawowe pojęcia
- Siła Lorentza: to siła działająca na ładunek elektryczny poruszający się w polu magnetycznym.
- Siła elektromotoryczna: to praca wykonana przez źródło na jednostkę ładunku, czyli „napięcie źródła” przy braku przepływu prądu.
Wzór na siłę Lorentza
Siła Lorentza jest maksymalna, gdy ruch ładunku jest prostopadły do pola magnetycznego, a zerowa, gdy ruch jest równoległy do pola.
$$F=q⋅v⋅B⋅sin0$$
Przykład:
Oblicz wartość siły działającej na ładunek $q=1,6⋅10^{-19}C$ poruszający się z prędkością $v=3⋅10^6 \frac{m}{s}$ prostopadle do pola magnetycznego o indukcji $B=0,02T$
Rozwiązanie:$$F=1,6⋅10^{-19}⋅3⋅10^6⋅0,02=9,6⋅10^{-15}N$$
Wzór na siłe elektromotoryczną
Siła elektromotoryczna to praca wykonana przez źródło na jednostkę ładunku, jest to „napięcie” źródła przy braku przepływu prądu.
$$ε=\frac{W}{q}$$
Przykład:
Źródło wykonuje pracę 100J, przenosząc ładunek 20C. Oblicz siłę elektromotoryczną.
Rozwiązanie:$$ε=\frac{100}{20}=5V$$
Indukcja elektromagnetyczna zachodzi, gdy zmienia się wartość lub kierunek pola magnetycznego przenikającego przez obwód elektryczny, co powoduje powstanie napięcia indukowanego, które może wywołać przepływ prądu indukcyjnego. To zjawisko jest opisane przez prawo Faradaya oraz regułę Lenza, ważne na maturze rozszerzonej.
Podstawowe pojęcia
- Indukcja elektromagnetyczna: to zjawisko powstawania siły elektromotorycznej (SEM) w obwodzie elektrycznym wskutek zmiany strumienia magnetycznego przepływającego przez ten obwód.
- Strumień magnetyczny: to iloczyn indukcji magnetycznej B przez pole powierzchni S prostopadłej do linii pola.
Wzór na strumień magnetyczny
Strumień magnetyczny mierzy, ile pola magnetycznego przepływa przez daną powierzchnię.
$$Φ=B⋅S⋅cos0$$
Przykład:
Wyznacz strumień magnetyczny dla pola o indukcji $0,5T$ przechodzącego przez powierzchnię prostokątną o powierzchni $0,2m^2$, gdy kąt $0 = 60^∘$.
Rozwiązanie:$$Φ=0,5⋅0,2⋅cos60^∘=0,5⋅0,2⋅0,5=0,05Wb$$
Prawo Faradaya
Siła elektromotoryczna jest proporcjonalna do szybkości zmiany strumienia magnetycznego i zawsze przeciwdziała tej zmianie.
$$E=-\frac{dΦ}{dt}$$
Przykład:
Wartość strumienia magnetycznego zmienia się ze 0,1Wb do 0,04Wb w czasie 0,02s. Oblicz wartość indukowanej siły elektromotorycznej.
Rozwiązanie:$$E=\frac{0,1-0,04}{0,02}=\frac{0,06}{0,02}=3V$$
Indukcja elektromagnetyczna w poruszającym się przewodniku
Przewodnik poruszający się w polu magnetycznym przecina linie pola, wytwarzając napięcie proporcjonalne do indukcji pola, prędkości i długości przewodnika.
$$E=B⋅v⋅l$$
Przykład:
Prosty przewodnik o długości $0,3 m$ porusza się z prędkością $2 \frac{m}{s}$ prostopadle do pola magnetycznego o indukcji $0,1 T$. Oblicz napięcie indukowane na końcach przewodnika.
Rozwiązanie:$$E=0,1⋅2⋅0,3=0,06V$$
Transformator jest urządzeniem elektrycznym służącym do zmiany wartości napięcia prądu przemiennego, działając na zasadzie indukcji elektromagnetycznej. Składa się z dwóch uzwojeń - pierwotnego i wtórnego - nawiniętych na wspólnym rdzeniu magnetycznym. Transformator pozwala efektywnie przesyłać energię elektryczną przy zmniejszeniu strat.
Podstawowe pojęcia
- Transformator: to urządzenie elektryczne, które zmienia wartość napięcia prądu przemiennego na inne, zachowując tę samą częstotliwość.
- Budowa transformatora: Zbudowany jest z dwóch uzwojeń: pierwotnego (podłączonego do źródła) i wtórnego (podłączonego do odbiornika), owiniętych na wspólnym rdzeniu magnetycznym.
Wzór na przekładnię transformatora
Stosunek napięć jest równy stosunkowi liczby zwojów uzwojeń.
$$\frac{U_1}{U_2}=\frac{n_1}{n_2}$$
Przykład:
Transformator ma 1200 zwojów w uzwojeniu pierwotnym i 300 zwojów w wtórnym. Oblicz napięcie na uzwojeniu wtórnym, jeśli na pierwotne podano 240 V.
Rozwiązanie:$$\frac{240}{U_2}=\frac{1200}{300}⟹U_2=\frac{240⋅300}{1200}=60V$$
Wzór na moc w transformatorze
Moc na wejściu transformatora jest równa mocy na wyjściu (w idealnym transformatorze).
$$P_1=P_2⇒U_1⋅I_1=U_2⋅I_2$$
Przykład:
Jeśli wtórne napięcie jest 60 V, a prąd 5 A, jaki jest prąd w uzwojeniu pierwotnym przy napięciu 240 V?
Rozwiązanie:$$I_1=\frac{U_2⋅I_2}{U_1}=\frac{60⋅5}{240}=1,25A$$
Fale mechaniczne potrzebują medium, przez które przenoszą energię. Fale elektromagnetyczne mogą rozchodzić się w próżni. W falach poprzecznych drgania są prostopadłe do kierunku rozchodzenia się fali, a w podłużnych - równoległe. Prędkość fali, jej długość oraz częstotliwość są podstawowymi wielkościami fizycznymi opisującymi fale.
Podstawowe pojęcia
- Fala: to rozchodzące się w ośrodku sprężystym zaburzenie przenoszące energię bez przeniesienia materii.
- Rodzaje fal: Wyróżniamy fale mechaniczne (potrzebują medium, np. fale dźwiękowe, fale na wodzie) oraz elektromagnetyczne (mogą przenikać przez próżnię, np. światło, fale radiowe). Ze względu na kierunek drgań względem kierunku rozchodzenia się fali wyróżniamy fale poprzeczne i podłużne.
Wzór na prędkość fali
Prędkość fali to stosunek długości fali do jej okresu lub iloczyn długości fali i częstotliwości.
$$v=\frac{λ}{T}=λ⋅f$$
Przykład:
Fala dźwiękowa ma długość $λ=0,34m$ i częstotliwości $f=1000Hz$. Oblicz prędkośc rozchodzenia się fali.
Rozwiązanie:$$v=λ⋅f=0,34⋅1000=340\frac{m}{s}$$
Wzór na długość fali
Długość fali to odległość między dwoma kolejnymi punktami o tej samej fazie.
$$λ=\frac{v}{f}$$
Przykład:
Fala elektromagnetyczna o częstotliwości $600 MHz$ rozchodzi się z prędkością światła $3⋅10^8\frac{m}{s}$. Oblicz długość fali.
Rozwiązanie:$$λ=\frac{3⋅10^8}{600⋅10^6}=0,5m$$
Wzór na okres fali
Okres to czas jednego pełnego drgania fali.
$$T=\frac{1}{f}$$
Przykład:
Fala ma częstotliwość 500 Hz. Oblicz jej okres.
Rozwiązanie:$$T=\frac{1}{500}=0,002s$$
